Lecture Notes 3: Solving Problem by Searching
Search

Can we solve the route problem from city A to city B using simple search like BFS?
A node in a tree typically have:
- STATE
- PARENT
- CHILDREN
Best-First Search
A node in Best-First Search typically have:
- STATE: the state in current node
- PARENT: the path or reference to the parent node consisting similar properties
- ACTION: the action of node that carried out
- PATH-COST: total cost from inital node until current node
Frontier is a queue that consist of:
- IS-EMPTY(frontier)
- POP(frontier)
- TOP(frontier)
- ADD(node, frontier)
The algorithm:
function BEST-FIRST-SEARCH(problem, f) returns a solution node or failure
node ← NODE(S TATE=problem.INITIAL)
frontier ← a priority queue ordered by f , with node as an element
reached ← a lookup table, with one entry with key problem.INITIAL and value node
while not IS-EMPTY(frontier) do
node ← POP(frontier)
if problem.IS-GOAL(node.STATE) then return node
for each child in EXPAND(problem, node) do
s ← child.STATE
if s is not in reached or child.PATH-COST < reached[s].PATH-COST then
reached[s] ← child
add child to frontier
return failure
function EXPAND( problem, node) yields nodes
s ← node.S TATE
for each action in problem.ACTIONS(s) do
s' ← problem.RESULT(s, action)
cost ← node.PATH-COST + problem.ACTION-COST(s, action, s0)
yield NODE(STATE=s' , PARENT=node, ACTION=action, PATH-COST=cost)
Measuring Problem-Solving Performance
- Completeness: This measurement ensure that the algorithm will return a solution or return “not found” if it does not have a solution.
- Cost Optimality: This will measure the cost or path to the solution. Ideally, low cost is preferrable
- Time Complexity: This will measure the duration or time for finding the solution.
- Space Complexity: This measure the space or memory to find the desired solution.
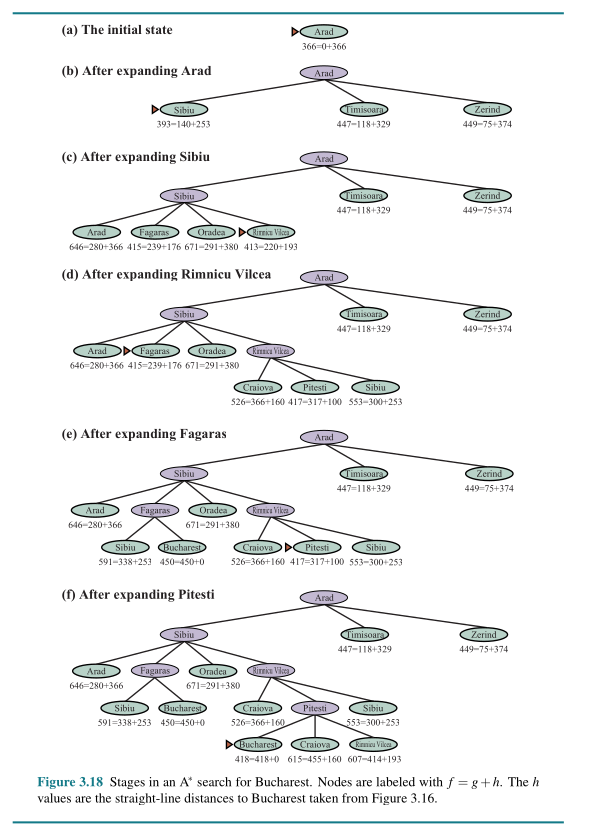
Informed (Heuristic) Search
The heuristic function is an estimated cost/fitness to the solution. For shortest distance, it can be the stright line.
Example of heuristic function for the shortest distance:

- Greedy best-first search

- A* search
\(g(n)\) is the actual cost and \(h(n)\) is the heuristic/estimated function
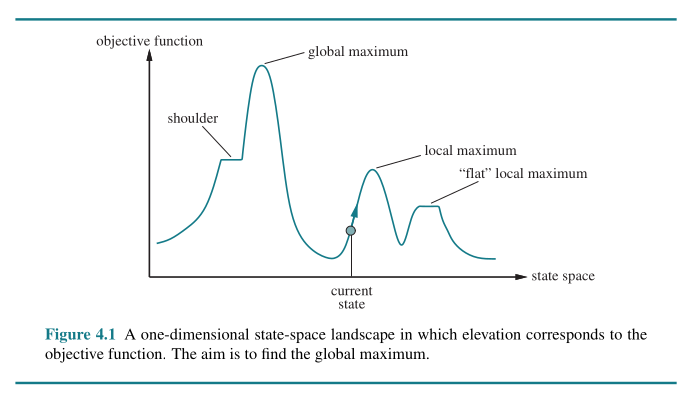
Local Search and Optimization Problem
Hill-Climbing Search
function HILL-CLIMBING(problem) returns a state that is a local maximum
current ← problem.INITIAL
while true do
neighbor ← a highest-valued successor state of current
if VALUE(neighbor) ≤ VALUE(current) then return current
current ← neighbor
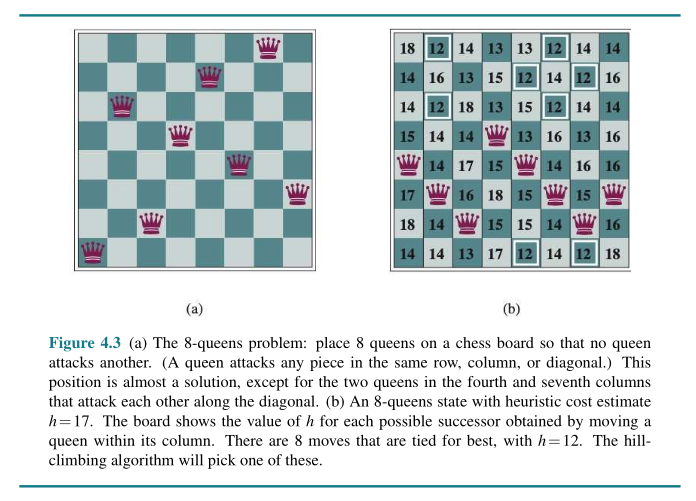
Please define the objective function..!?
Global Search
Simulated Annealing: Single-Based Solution
function SIMULATED-ANNEALING(problem, schedule) returns a solution state
current ← problem.INITIAL
for t = 1 to ∞ do
T ← schedule(t)
if T = 0 then return current
next ← a randomly selected successor of current
∆E ← VALUE(current) – VALUE(next)
if ∆E > 0 then current ← next
else current ← next only with probability e^{∆E/T}
Genetic Algorithm: Population-Based Solution
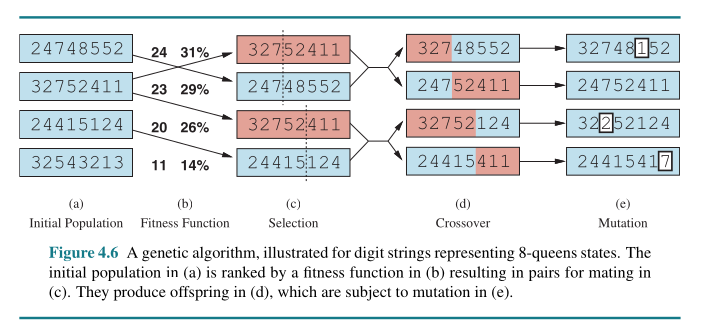
function GENETIC-ALGORITHM(population, fitness) returns an individual
repeat
weights ← WEIGHTED-BY(population, fitness)
population2 ← empty list
for i = 1 to SIZE(population) do
parent1, parent2 ← WEIGHTED-RANDOM-CHOICES(population, weights, 2)
child ← REPRODUCE(parent1, parent2)
if (small random probability) then child ← MUTATE(child)
add child to population2
population ← population2
until some individual is fit enough, or enough time has elapsed
return the best individual in population, according to fitness
function REPRODUCE(parent1, parent2) returns an individual
n ← LENGTH(parent1)
c ← random number from 1 to n
return APPEND(SUBSTRING(parent1, 1, c), SUBSTRING(parent2, c + 1, n))
Exercise
Please submit the assingment before 7 October 2025 (Week 5).
Please implement the genetic algorithm to find the optimal course schedule in informatics! The students need to specify the solution representation, the objective function, reproduction/recombination mechanism, and mutation mechanism. Please run for several generation (let say 30-100).
The chapter should includes:
- Solution Representation, Objective, and Genetic Operators (how solution is being presented? how the objective/fitness function is defined? how genetic operator behave on your solution representation?)
- Implementation (the code with the line numbers, the students have to explain the code by the line numbers)
- Results (the students should show the results of the program, how it can be used? until it produce the solution)
- Conclusion