Lecture Notes 4: Adversarial Search and Games

When two or more agents pursue conflicting goals, a problem known as adversarial search arises. In this lecture, we will explore how agents operate in competitive environments, where each agent must reason about and respond to the actions of others to achieve its objective.

Two-player zero-sum games

zero-sum games means that there is unlikely to have multiple winners which means that what is good for one entitiy is bad for the others.

For agent in games the synonym for action and state are move and position respectively.

• \(S_0\) is the initial state, the starting condition of a game
• TO-MOVE(s): player whose turn it is to move in state s
• ACTIONS(s): the set of legal moves in state s
• RESULT(s, a) is a transition model that defines the state resulting from taking action a in state s
• IS-TERMINAL(s) is a terminal test which is true when the game is over and false otherwise
• UTILITY(s, p) is a utility function (can be considered as objective function). This provide numerical value to player p when in terminate state s (the game ends). In case of chess the outcomes are win (1), loss (0), or draw (0.5)

MINIMAX Search Algorithm

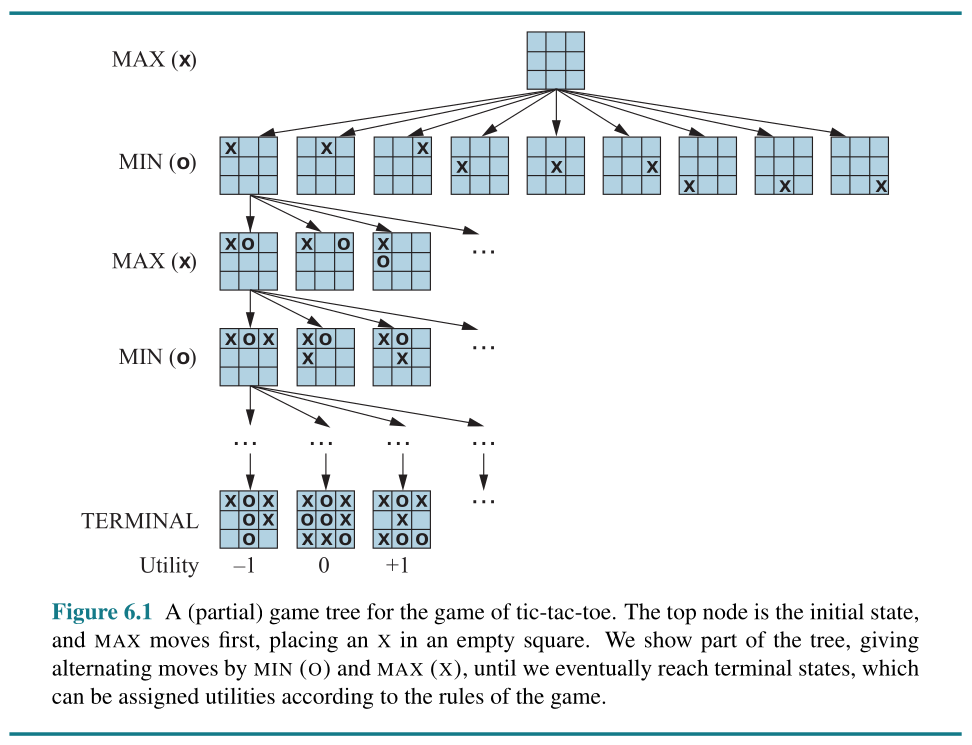
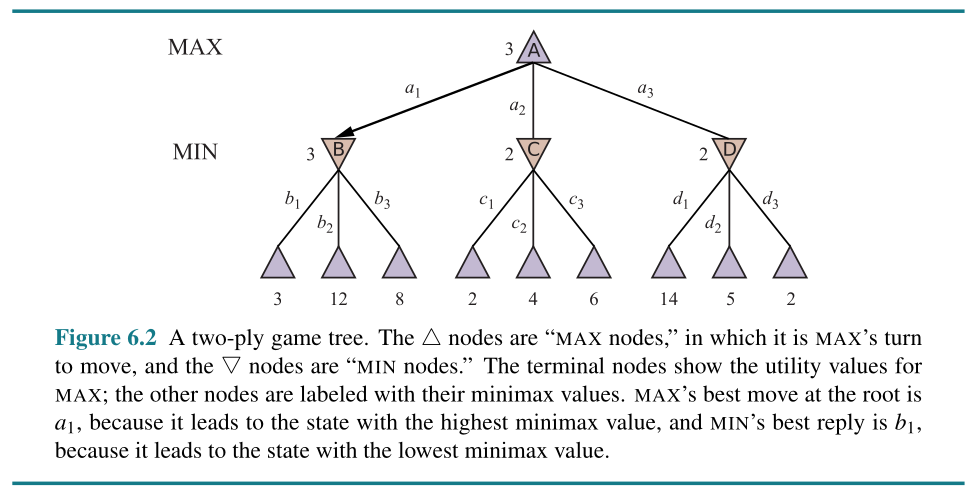
The algorithm:

function MINIMAX-SEARCH(game, state) returns an action
    player ← game.TO-MOVE(state)
    value, move ← MAX-VALUE(game, state)
    return move

function MAX-VALUE(game, state) returns a (utility, move) pair
    if game.IS-TERMINAL(state) then return game.UTILITY(state, player), null
    v, move ← −∞
    for each a in game.ACTIONS(state) do
        v2, a2 ← MIN-VALUE(game, game.RESULT(state, a))
        if v2 > v then
            v, move ← v2, a
    return v, move

function MIN-VALUE(game, state) returns a (utility, move) pair
    if game.IS-TERMINAL(state) then return game.UTILITY(state, player), null
    v, move ← +∞
    for each a in game.ACTIONS(state) do
        v2, a2 ← MAX-VALUE(game, game.RESULT(state, a))
        if v2 < v then
            v, move ← v2, a
    return v, move

If there is \(b\) legal move with the maximum depth of a tree \(m\), then the time complexity is \(\mathcal{O}(b^m)\)

“The space complexity is \(\mathcal{O}(bm)\) for an algorithm that generates all actions at once”

Alpha–Beta Pruning in MINIMAX search

In MINIMAX search wihthout pruning, all tree must be visited. In alpha-beta pruning, only reasonable node that will be visited, avoiding unnecessary computation.

α = the value of the best (i.e., highest-value) choice we have found so far at any choice point along the path for MAX. Think: α = “at least.”

β = the value of the best (i.e., lowest-value) choice we have found so far at any choice point along the path for MIN. Think: β = “at most.”

Let see an example…

The algorithm:

function ALPHA-BETA-SEARCH(game, state) returns an action
    player ← game.TO-MOVE(state)
    value, move ← MAX-VALUE(game, state, −∞, +∞)
    return move

function MAX-VALUE(game, state, α, β) returns a (utility, move) pair
    if game.IS-TERMINAL(state) then return game.UTILITY(state, player), null
    v ← −∞
    for each a in game.ACTIONS(state) do
        v2, a2 ← MIN-VALUE(game, game.RESULT(state, a), α, β)
        if v2 > v then
            v, move ← v2, a
            α ← MAX(α, v)
        if v ≥ β then return v, move
    return v, move

function MIN-VALUE(game, state, α, β) returns a (utility, move) pair
    if game.IS-TERMINAL(state) then return game.UTILITY(state, player), null
    v ← +∞
    for each a in game.ACTIONS(state) do
        v2, a2 ← MAX-VALUE(game, game.RESULT(state, a), α, β)
        if v2 < v then
        v, move ← v2, a
        β ← MIN(β, v)
        if v ≤ α then return v, move
    return v, move

“If this could be done perfectly, alpha–beta would need to examine only \(\mathcal{O}(b^{\frac{m}{2}})\) nodes to m pick the best move, instead of O(b) for minimax.”

Heuristic Alpha–Beta Tree Search

s = state; d = depth

Evaluation Functions

What the things to consider to form a good evaluation functions?

1. The eval function should not take too long.
2. The eval function should highly related to the chance of winning.

weighted linear function:

for example in chess book, approximate material value: pawn worth 1, knight or bishop worth 3, a rook 5, a queen 9.

each \(f_i\) is a feature of the position (such as “number of white bishops”) and each \(w_i\) is a weight (saying how important that feature is). The weights should be normalized so that the sum is always within the range of a loss (0) to a win (+1).

Monte Carlo tree search (MCTS)

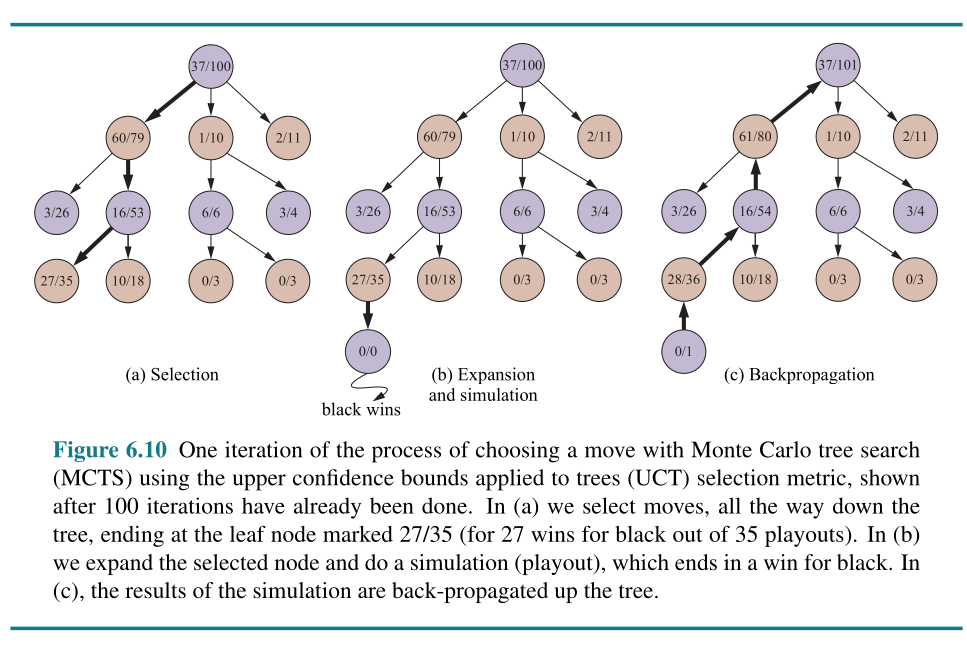
Algorithm of MCTS:

function MONTE-CARLO-TREE-SEARCH(state) returns an action
    tree ← NODE(state)
    while IS-TIME-REMAINING() do
    leaf ← SELECT(tree)
    child ← EXPAND(leaf)
    result ← SIMULATE(child)
    BACK-PROPAGATE(result, child)
    return the move in ACTIONS(state) whose node has highest number of playouts

where:

• \(\bar{X}_j\) = average reward for child \(j\)
• \(n\) = number of times the parent node has been visited
• \(n_j\) = number of times child \(j\) has been visited
• \(c\) = exploration constant (typically \(\sqrt{2}\))